全等三角形的10个模型

一笑而过

一、倍长中线模型

1、基本模型

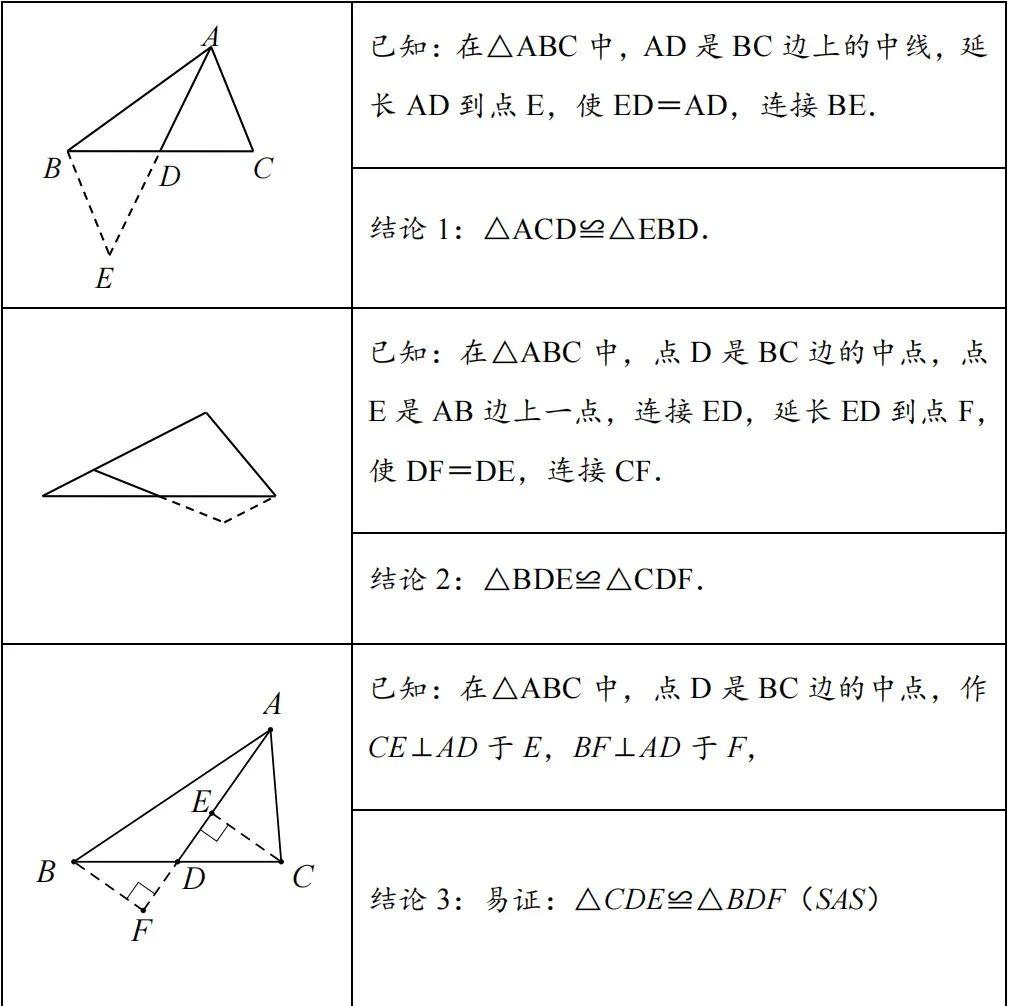
2、结论推导

3、解题技巧

遇到中点或中线，则考虑使用“倍长中线模型”，即延长中线，使所延长部分与中线相等，然后连接相应的顶点，构造出全等三角形．

4、历史文章

一题多解 | 中线倍长；

来解题吧 | 逆用倍长中线；

来解题吧 | 逆用倍长中线+翻折求最值；

二、一线三等线模型‍‍

1、基本模型

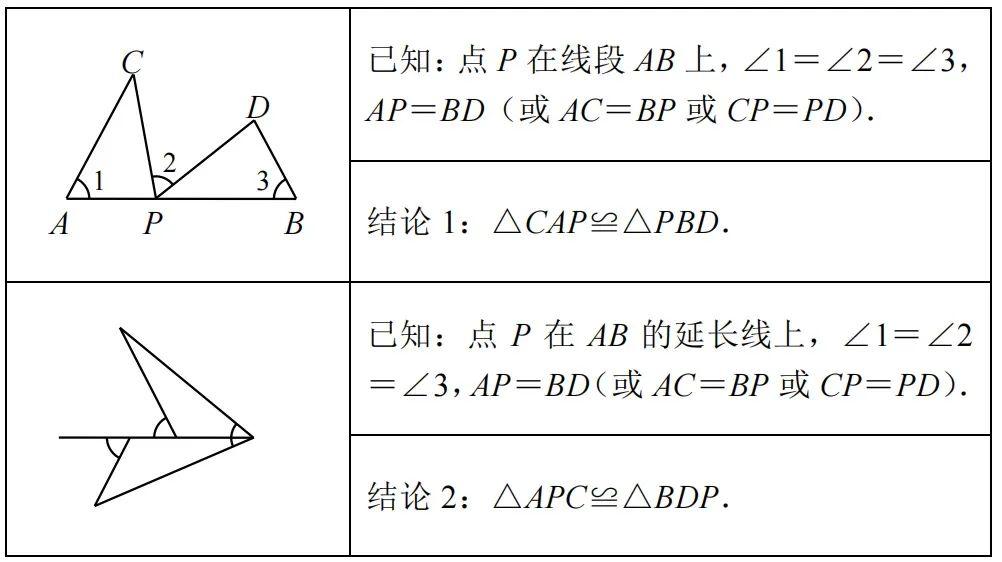
2、结论推导

结论1：△CAP≌△PBD．

证明：∵∠1＋∠C＋∠APC＝180°，∠2＋∠BPD＋∠APC＝180°，∠1＝∠2，∴∠C＝∠BPD．

∵∠1＝∠3，AP＝BD（或AC＝BP或CP＝PD），∴△CAP≌△PBD．

结论2：△APC≌△BDP．

证明：∵∠1＝∠C＋∠APC，∠2＝∠BPD＋∠D，∠3＝∠BPD＋∠APC，∠1＝∠2＝∠3，

∴∠C＝∠BPD，∠APC＝∠D．∵AP＝BD（或AC＝BP或CP＝PD），∴△APC≌△BDP．

3、解题技巧

在一条线段上出现三个相等的角，且有一组边相等时，则考虑使用一线三等角全等模型．找准三个等角，再根据平角性质、三角形内角和进行等角代换，判定三角形全等，然后利用全等三角形的性质解题．一线三等角模型常以等腰三角形、等边三角形、四边形（正方形或矩形）为背景，在几何综合题中考查．

4、历史文章

初中数学 | 一线三等角

趣味几何｜构造一线三等角、结合不定方程求解反比例函数k值

来解题吧 | 一线三等角

三、半角模型

1、基本模型

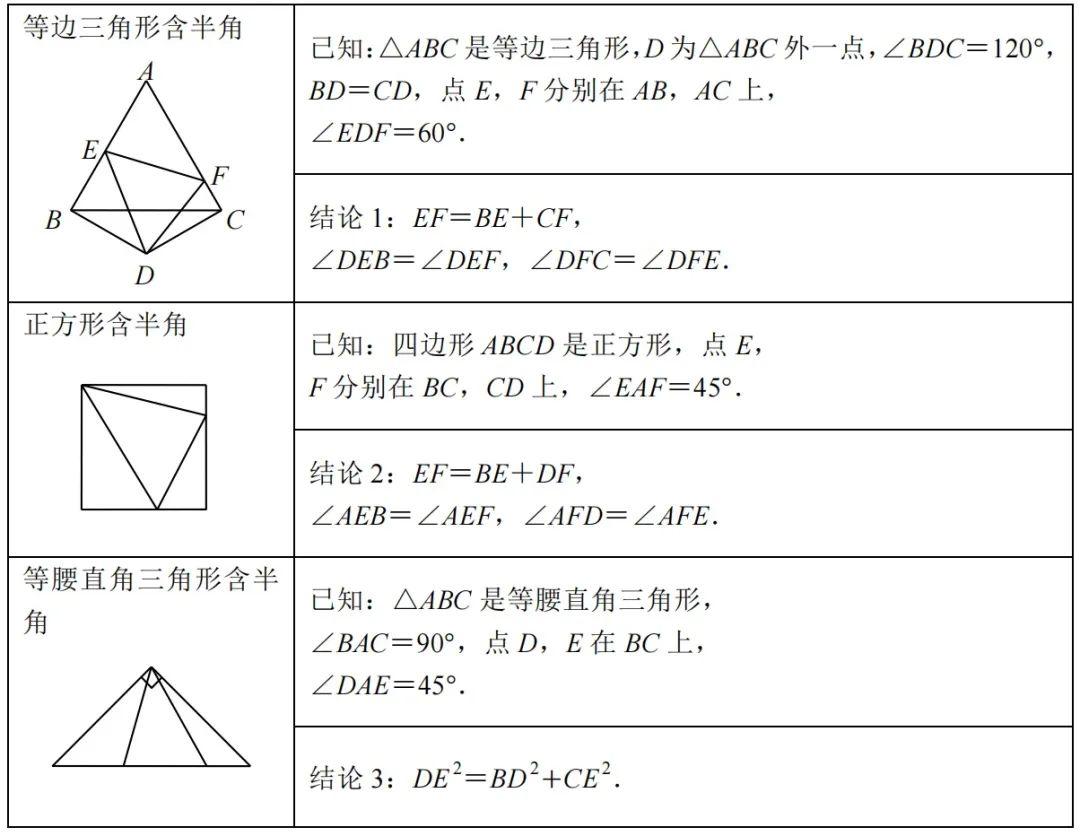
2、结论推导‍

3、解题技巧

对于半角模型，一般情况下都需要做辅助线（延长或旋转），构造全等，通过等量代换得到相关的结论．

4、历史文章

初中几何｜半角模型

来解题吧 | 半角模型与费马点完美结合

四、手拉手模型

1、基本模型

2、结论推导

3、解题技巧

如果题目中出现两个等腰三角形，可以考虑连接对应的顶点，用旋转全等模型；如果只出现一个等腰三角形，可以用旋转的方法构造旋转全等．

4、历史文章

几何模型 | 手拉手模型

趣味几何｜逆推问题寻思路，巧妙构造“手拉手”

初中数学 | 手拉手模型的应用

五、对角互补模型

1、基本模型

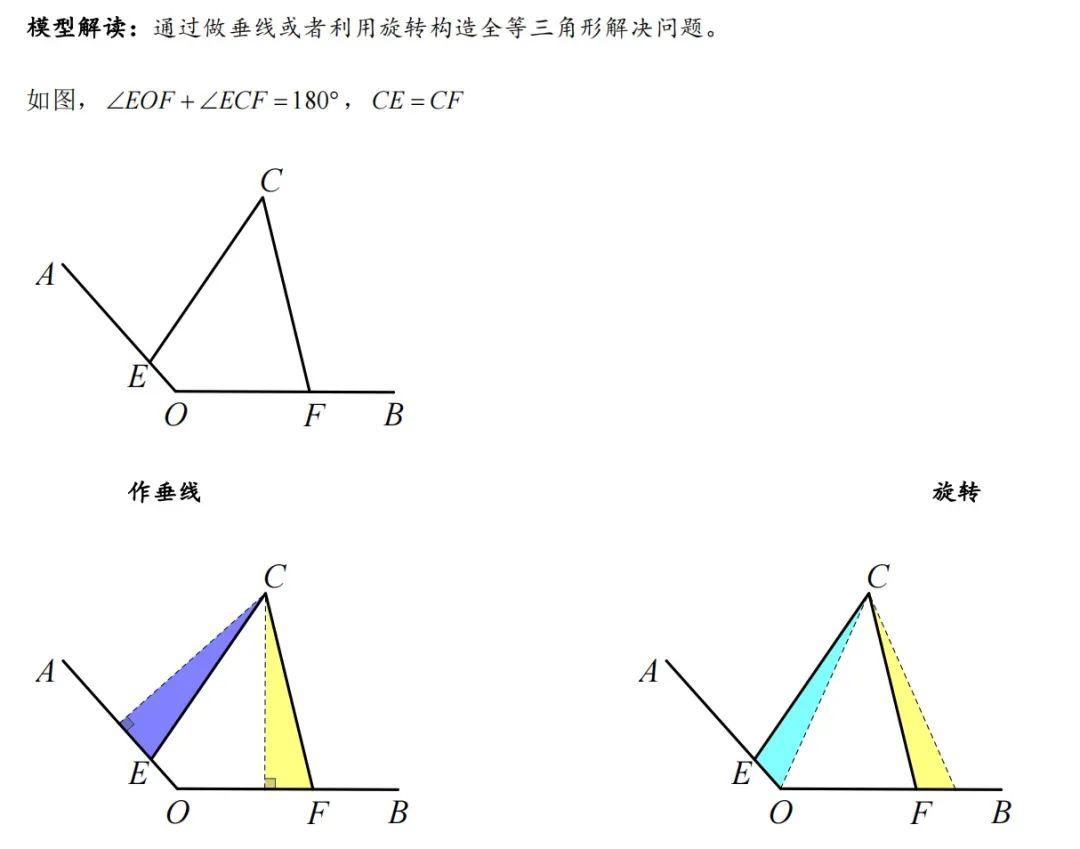
2、历史文章

几何模型｜对角互补模型之120°等腰三角形

几何模型｜对角互补模型之任意角α

六、平行线夹中点模型

1、模型结论

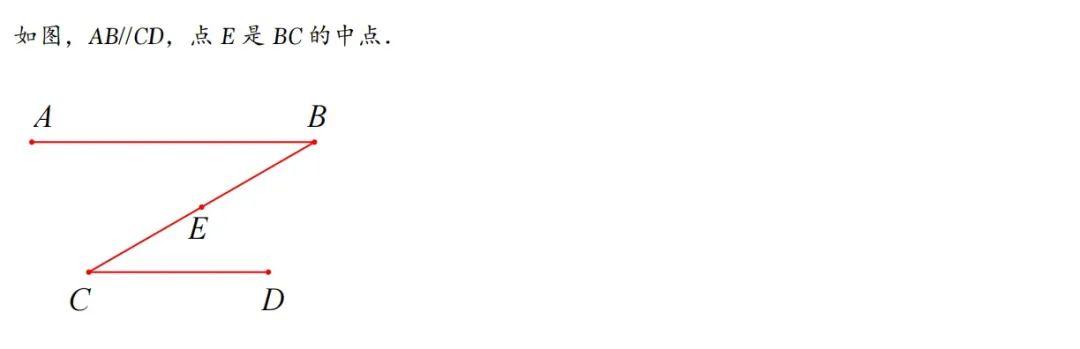
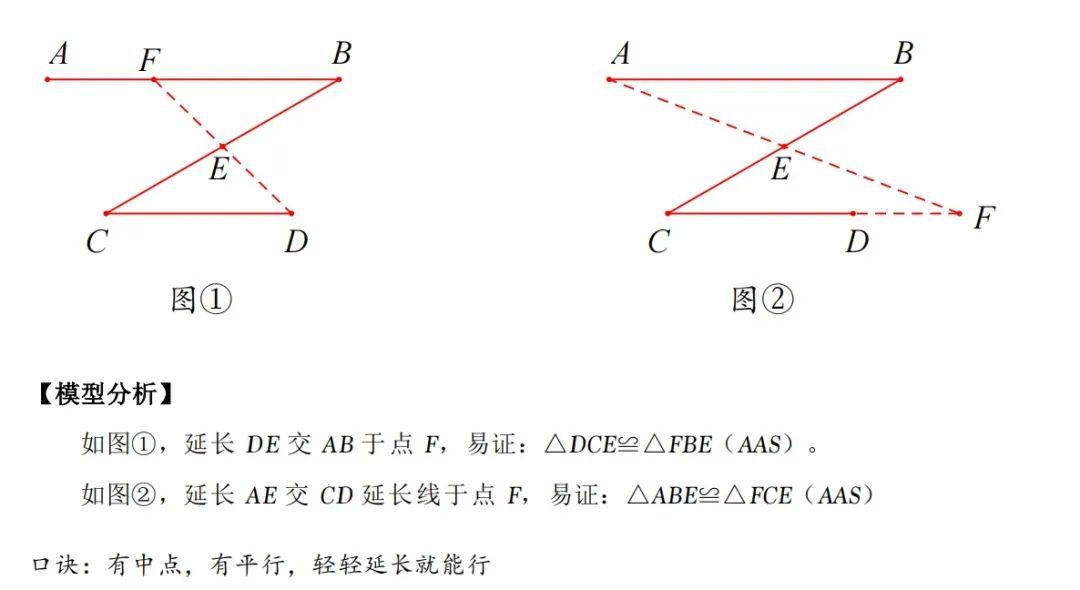
2、历史文章

平行线夹中点辅助线方法

七、截长补短模型

1、模型结论

【模型解读】截长补短的方法适用于求证线段的和差倍分关系。截长:指在长线段中截取一段等于已知线段:补短:指将短线段延长,延长部分等于已知线段。该类题目中常出现等服三角形、角平分线等关键词句,可以采用截长补短法构造全等三角形来完成证明过程,截长补短法(往往需证2次全等)。

2、历史文章

一题多解｜截长补短问题6种证明方法

八、绝配角模型

1、基本模型‍‍‍

2、结论推导

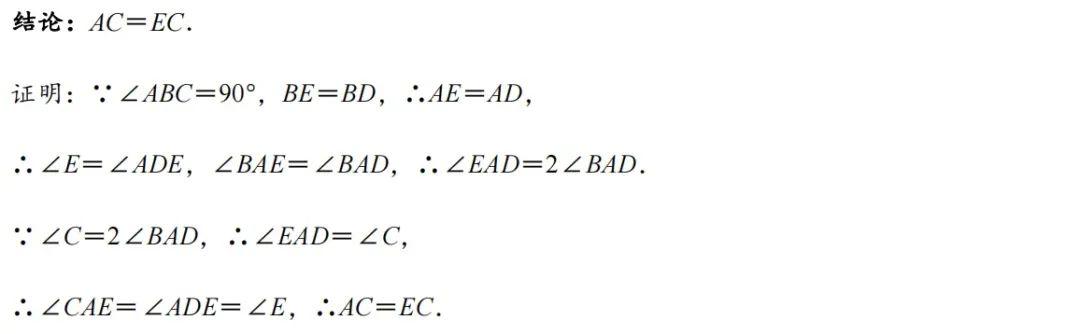
3、解题技巧

如果题目中出现二倍角，可以考虑用绝配角模型，构造等腰三角形，绝配角＋等腰三角形＋全等三角形一般同时出现，然后用勾股定理或相似求解．构造等腰三角形是这类绝配角问题的重要方法．

4、历史文章

来解题吧 | 绝配角在几何解题中的应用

九、婆罗摩笈多模型‍‍

1、基本模型

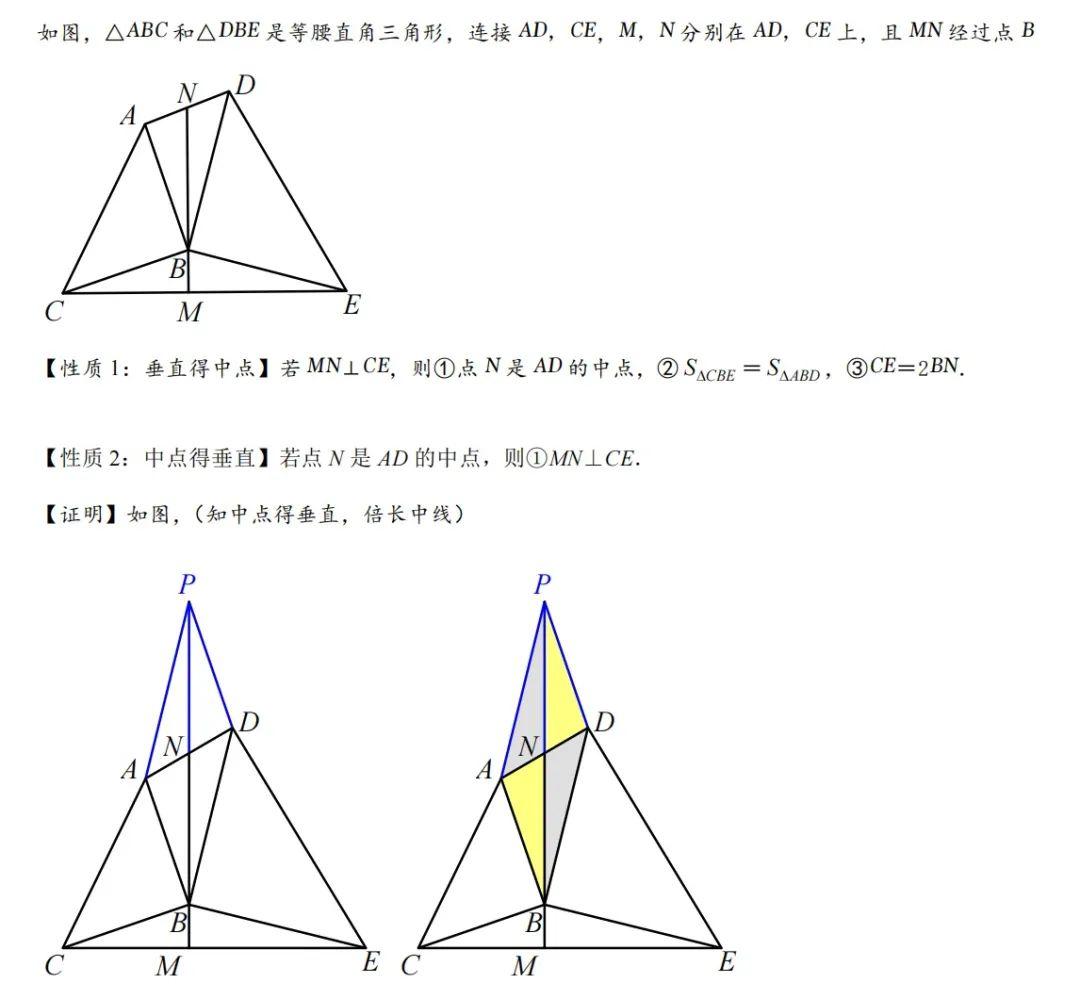
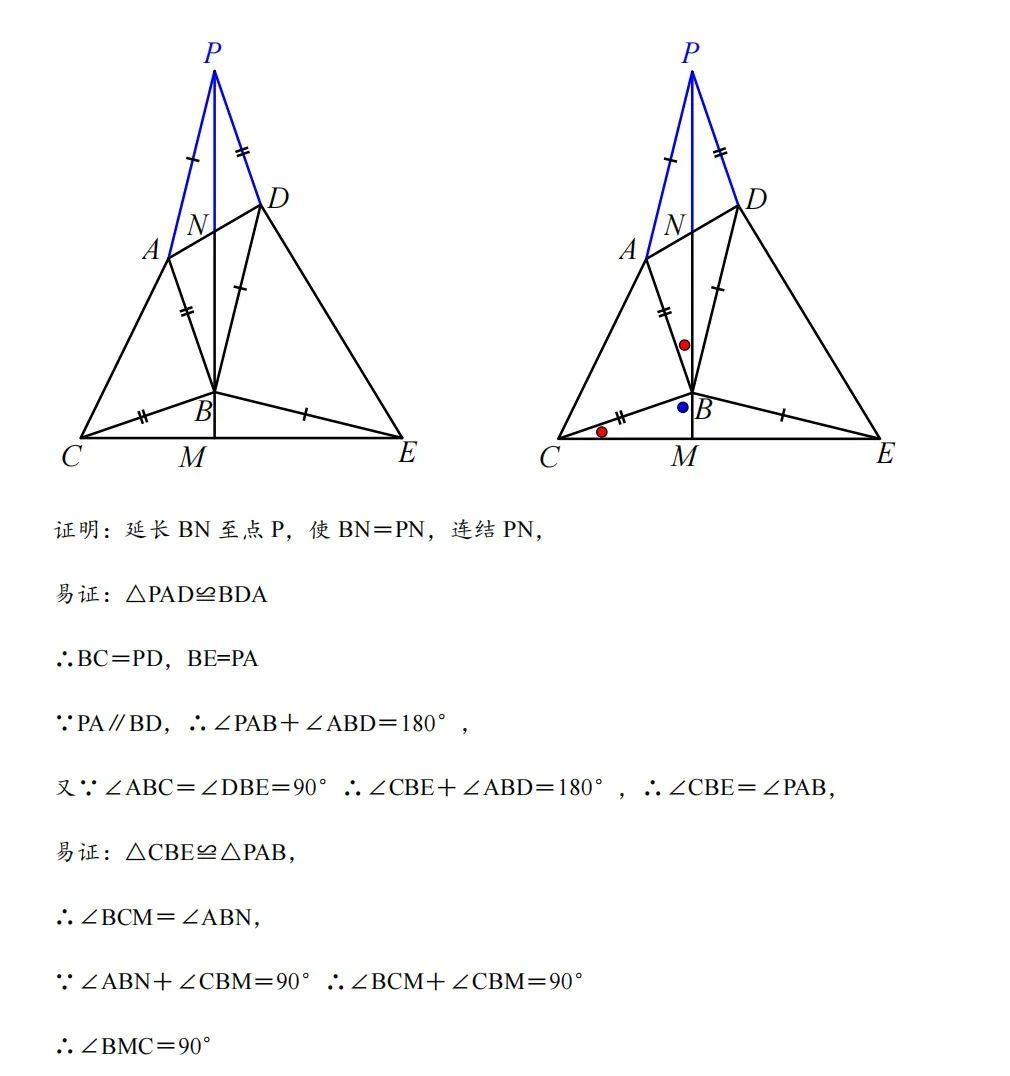
2、历史文章

几何模型 | 婆罗摩笈多定理&模型&公式

十、海岛埋宝模型

1、基本模型
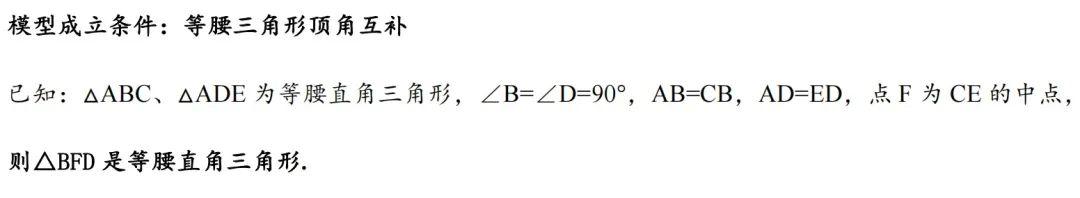
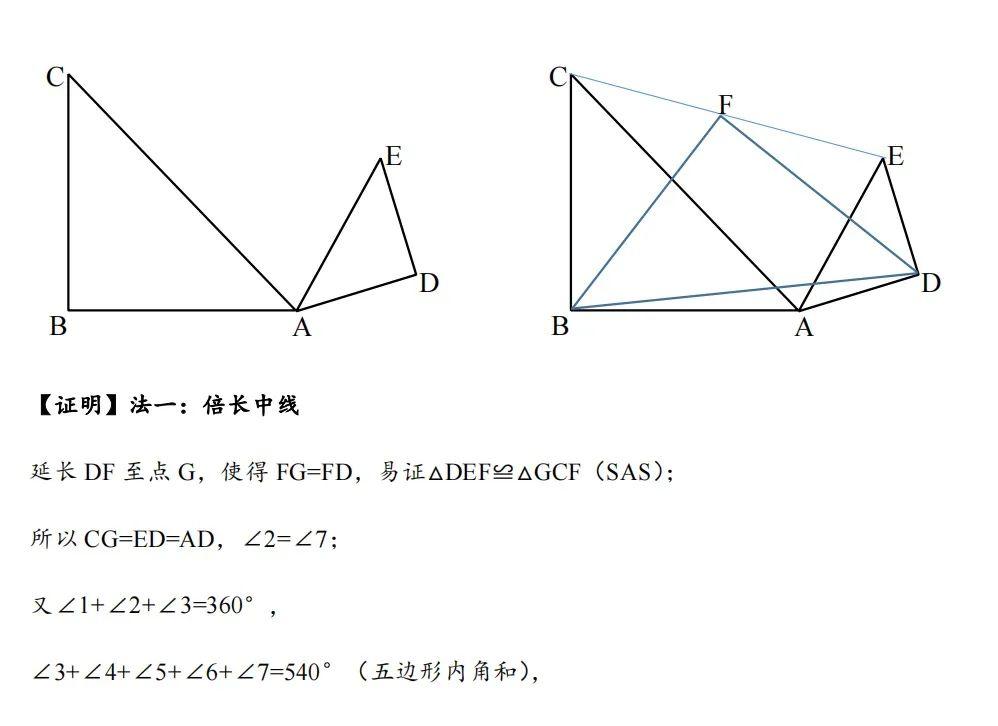
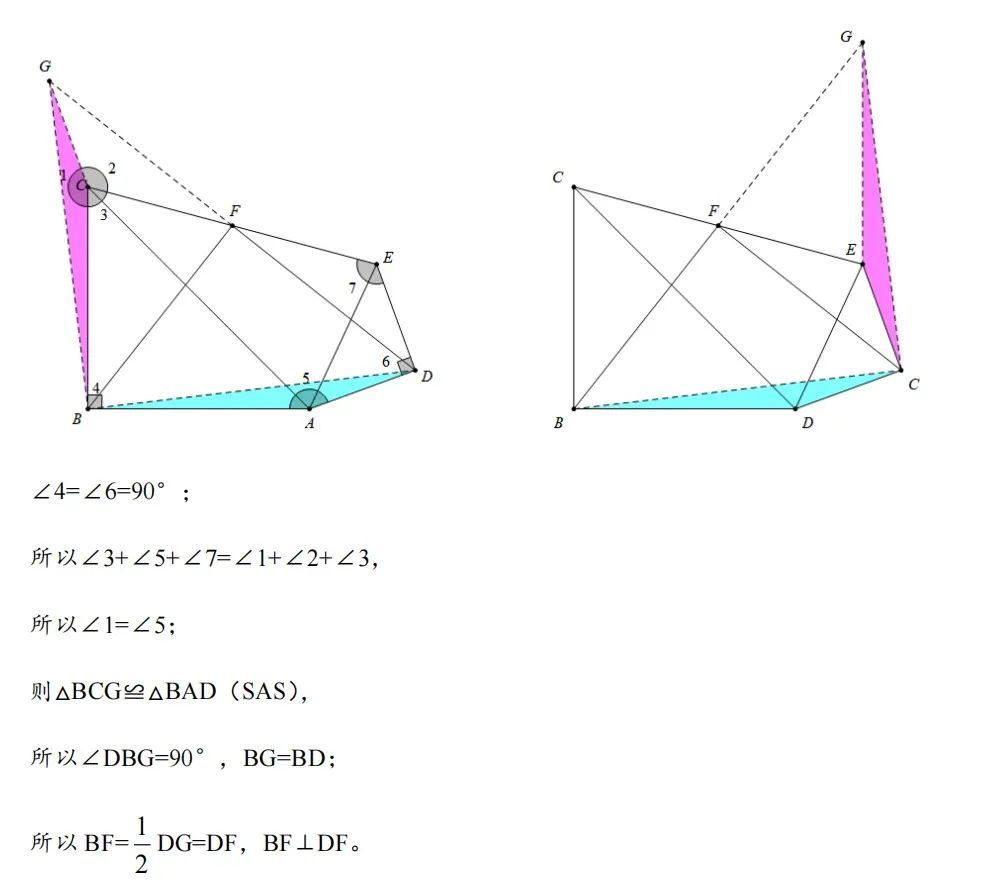